Vector-MKdV Solitons I
Vector MKdV Equation ut + 24|u|2ux + uxxx = 0
In vector notation, u = (u1,...,uN) is a N-component variable satisfying the vector MKdV equationFor the special case when N=2, this vector equation is equivalent to the Hirota-MKdV equation
1-Soliton Solution
Travelling waves are given by the 1-soliton solution2-Soliton Solution
Collisions where a fast travelling wave with speed c1 and orientation (unit vector) φ1 overtakes a slow travelling wave with speed c2 and orientation (unit vector) φ2 are given by the 2-soliton solutionF= 4√c1√c2 φ1⋅φ2 + (√c1 − √c2)2 cosh(√c1 ξ1 + √c2 ξ2) + (√c1 + √c2)2 cosh(√c1 ξ1 − √c2 ξ2)
where ξ1 = x−c1t, ξ2 = x−c2t are moving coordinates.
Interaction Properties
Depending on their speed ratio c1/c2 and relative orientation angle Δφ = arccos(φ1⋅φ2), the fast and slow waves in a collision exhibit three different types of nonlinear interactions.1) Merge-Split: the waves first merge together at t=x=0 and then split apart into their original shapes and speeds.
2) Bounce-Exchange: the waves first bounce and then exchange their shapes and speeds at t=x=0.
3) Absorb-Emit: the fast wave gradually first absorbs and then emits the slow wave.
In all three types of interactions, the waves emerging from the collision retain the shape, speed, and orientation of the initial two waves. The only remnant of the interaction is a forward shift in the position of the faster wave
and a backward shift in the position of the slower wave
where these position shifts depend only on the speeds of the waves but not on their orientations.
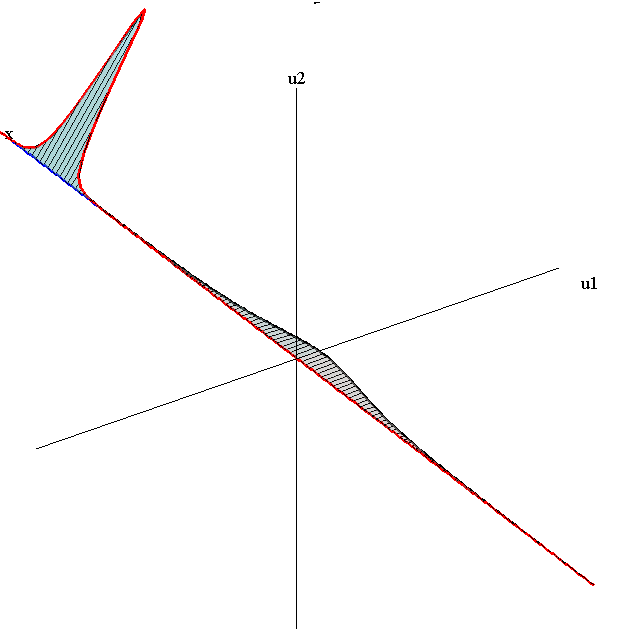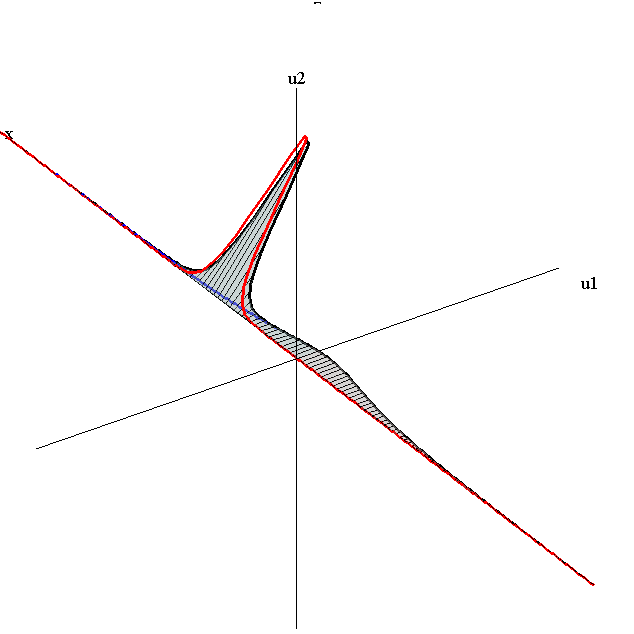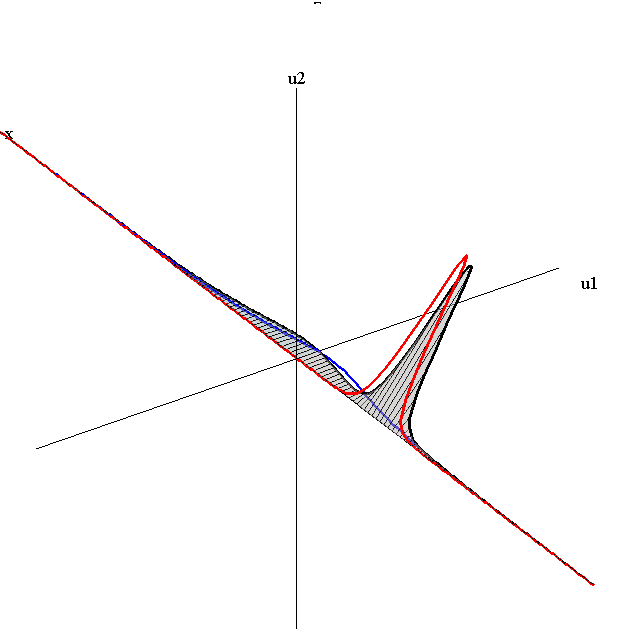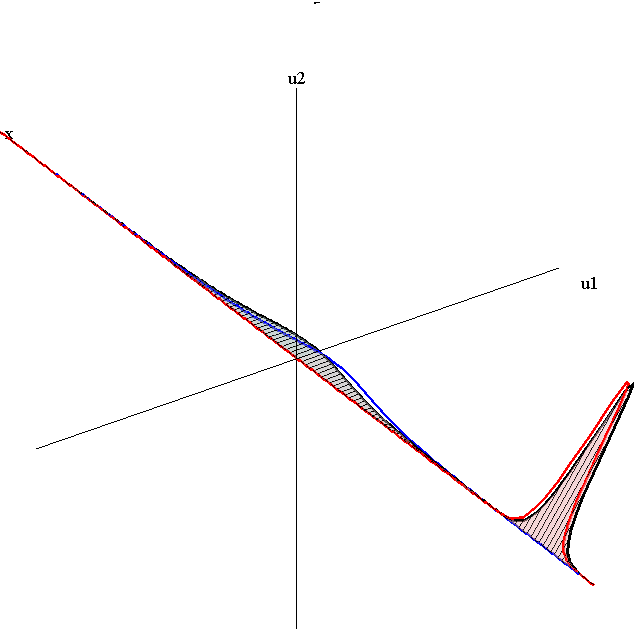
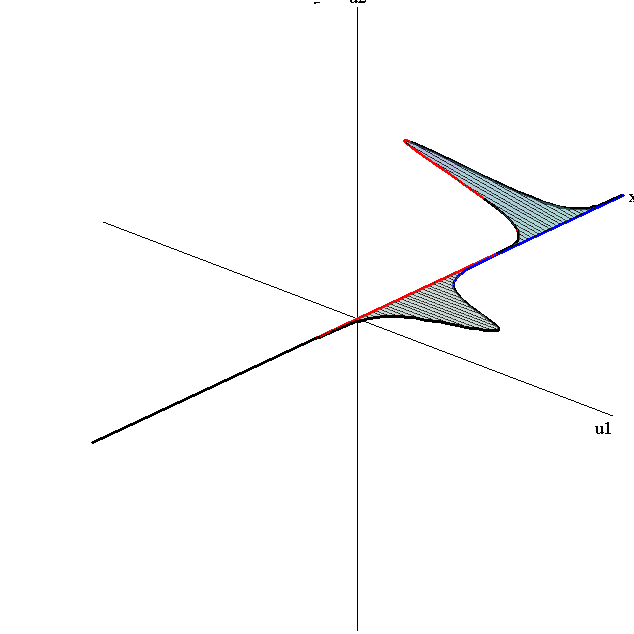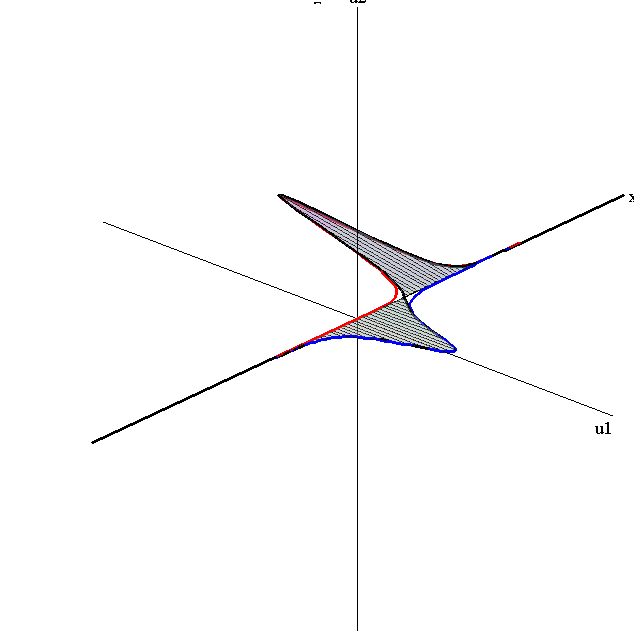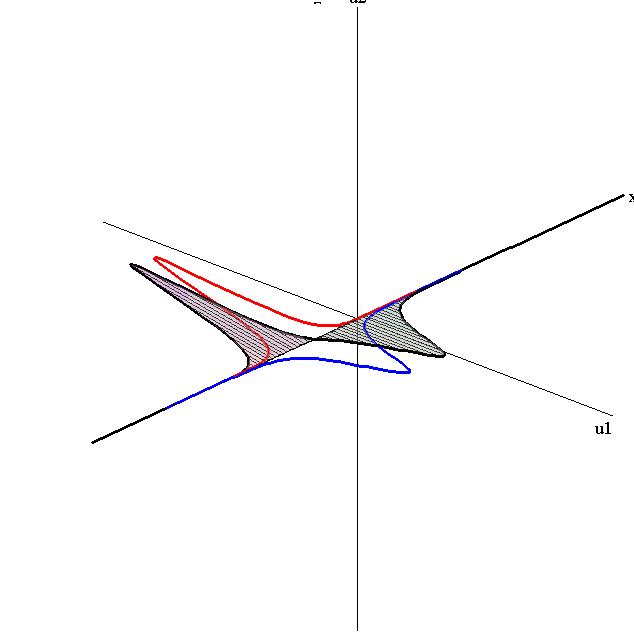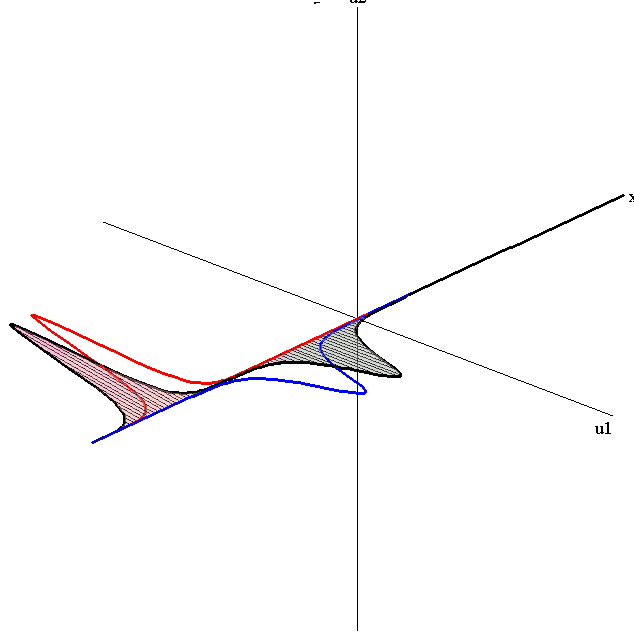
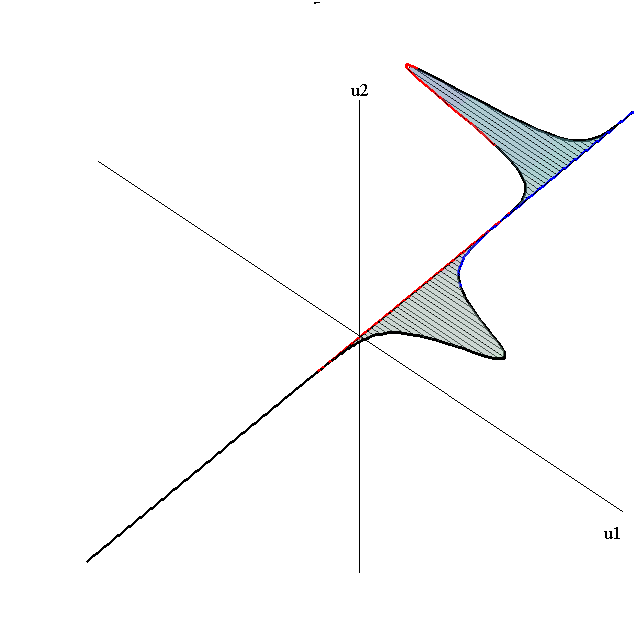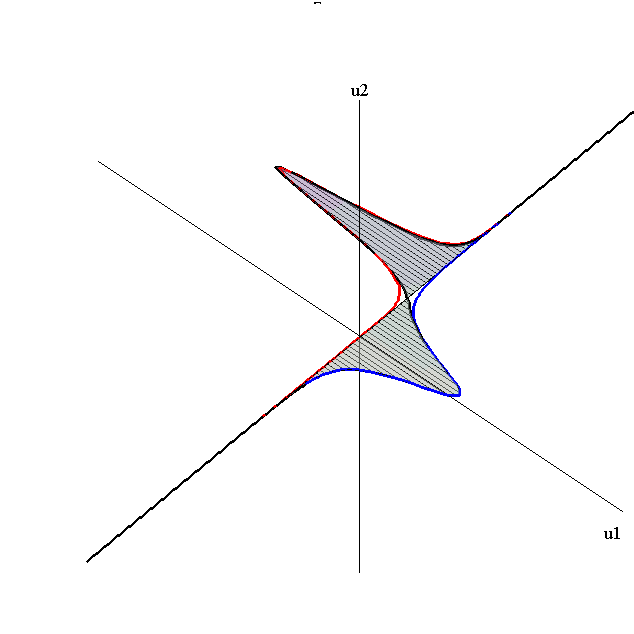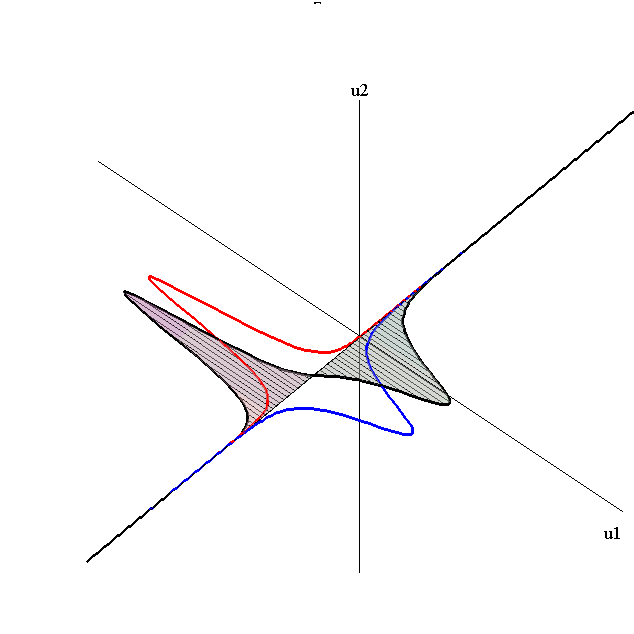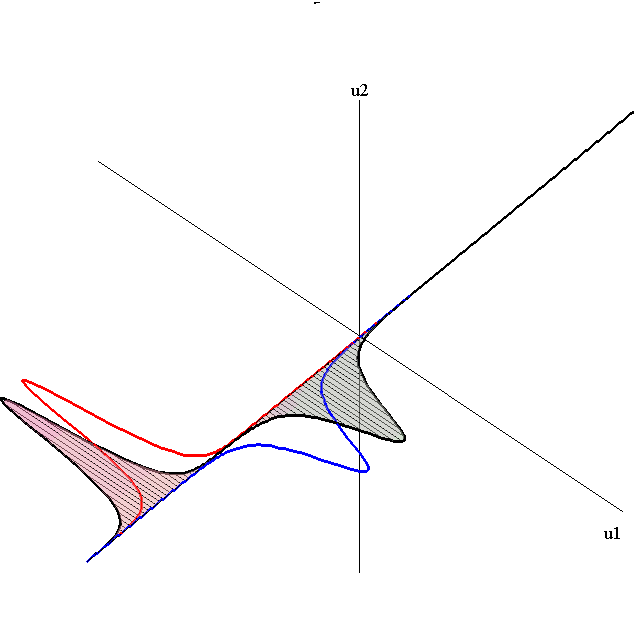
Overlay of 1-Soliton Solutions and Corresponding 2-Soliton Solution
Merge-Split Interaction
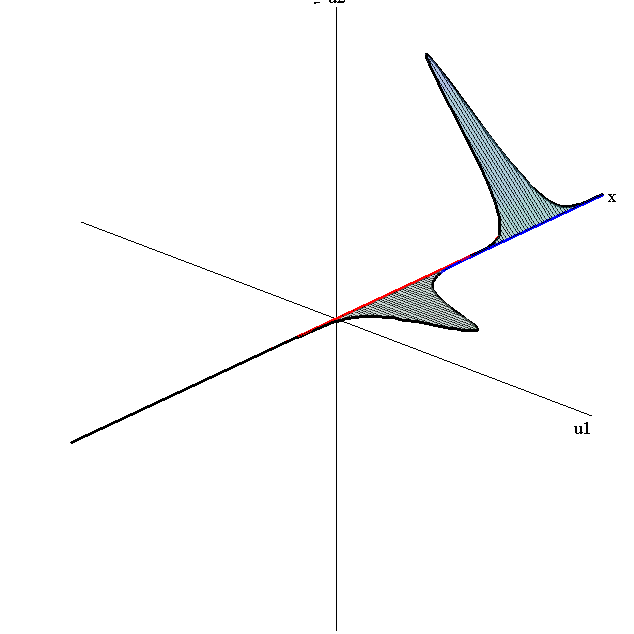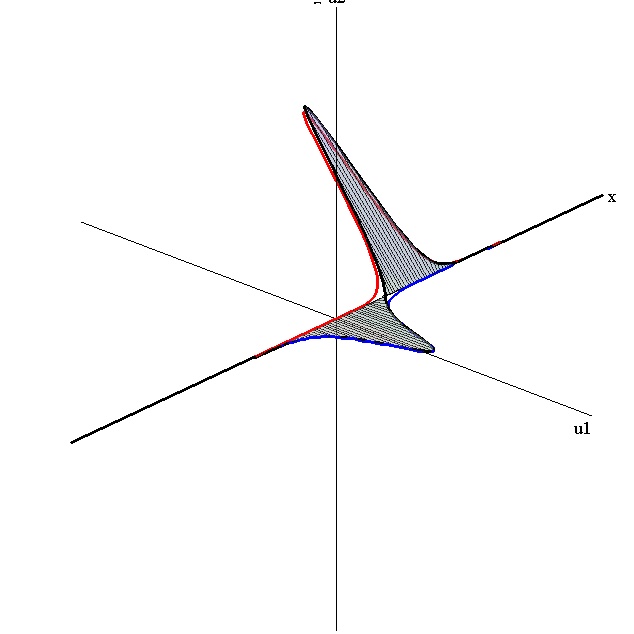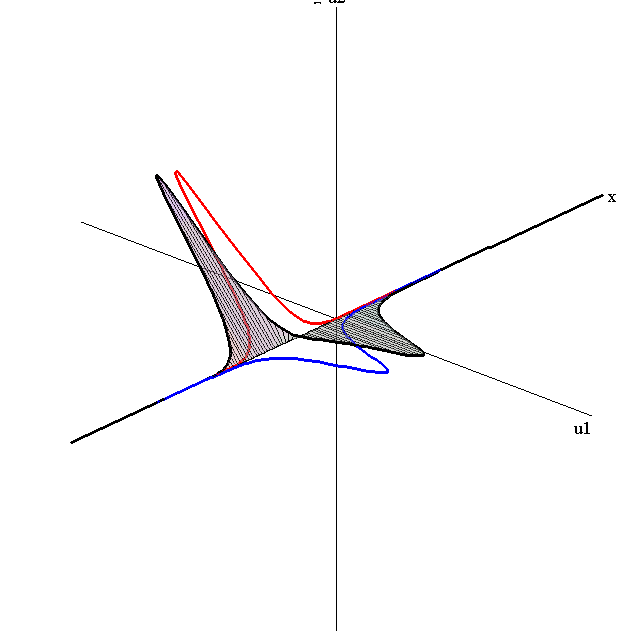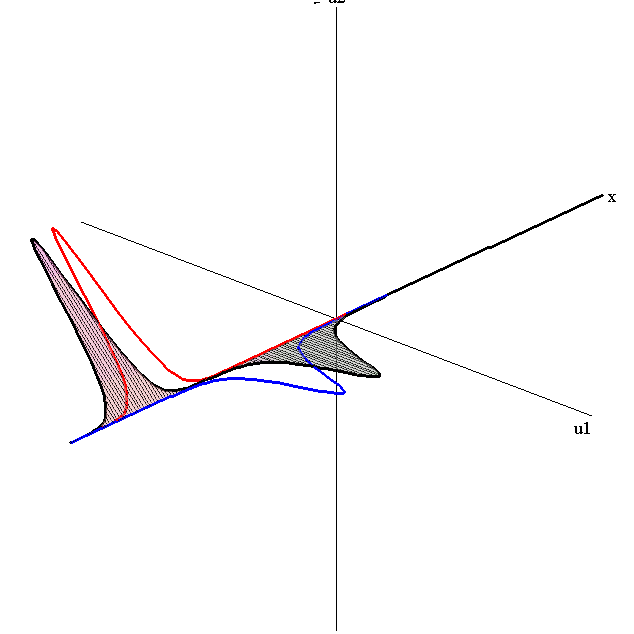
speed ratio: c1/c2 = 2.8
relative orientation angle: Δφ = 0.75 π
speed ratio: c1/c2 = 50
relative orientation angle: Δφ = 0.3 π
Bounce-Exchange Interaction
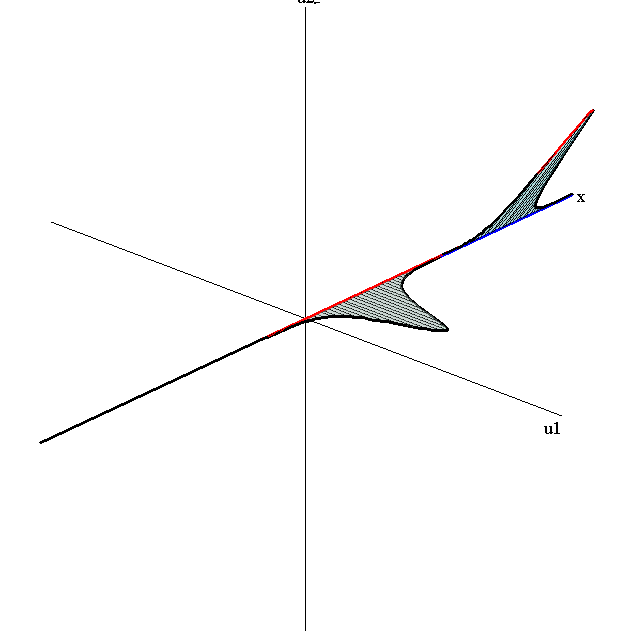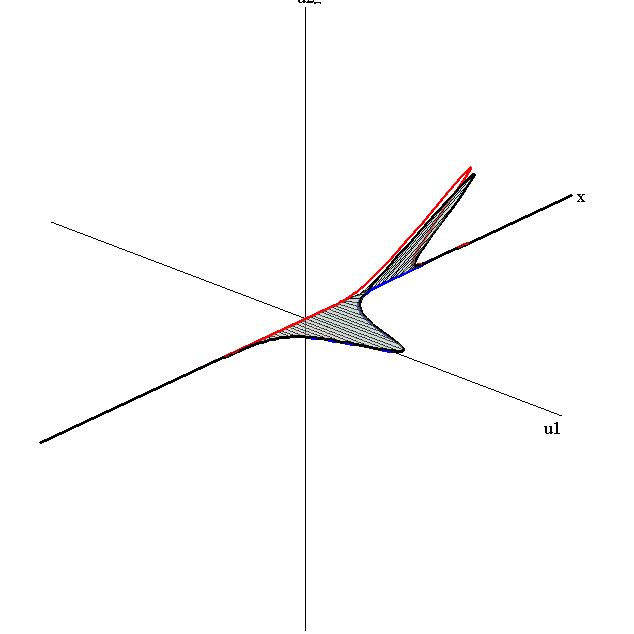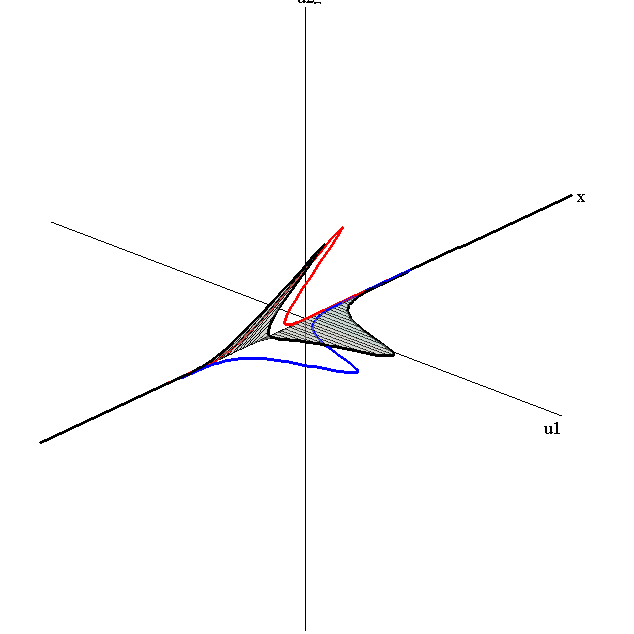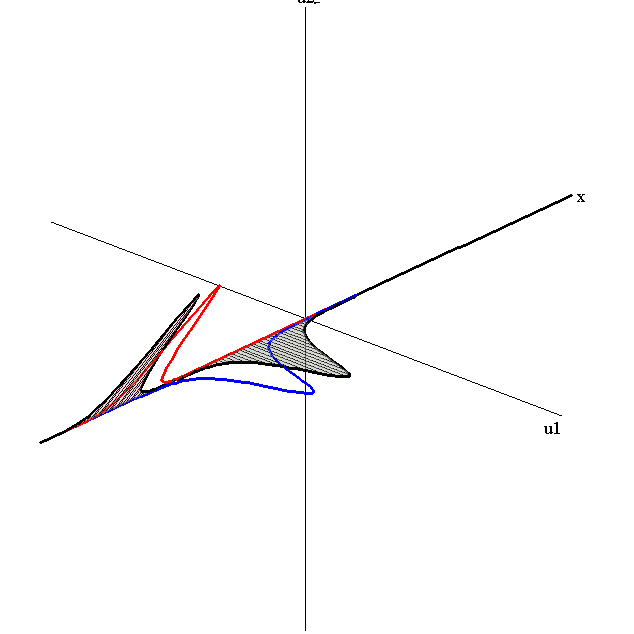
speed ratio: c1/c2 = 2.8
relative orientation angle: Δφ = 0.3 π
Absorb-Emit interaction
speed ratio: c1/c2 = 2.8
relative orientation angle: Δφ = 0.95 π
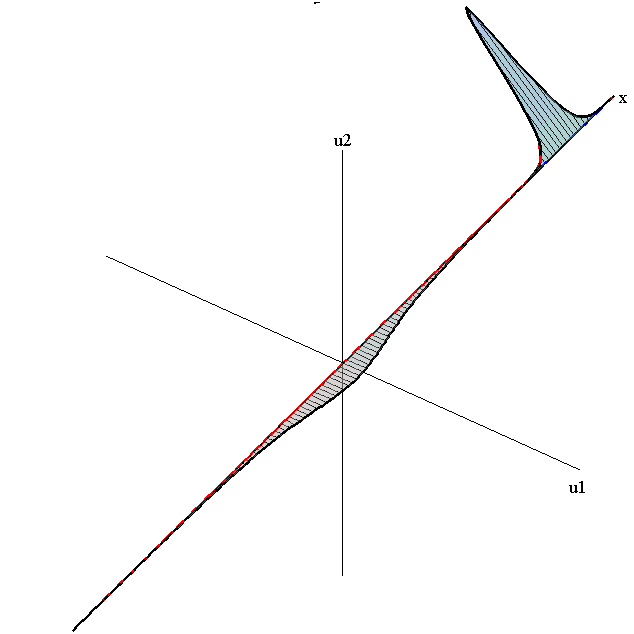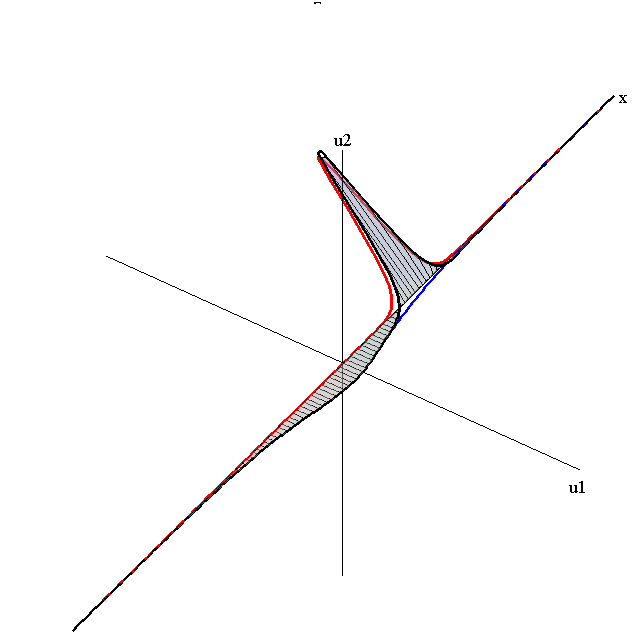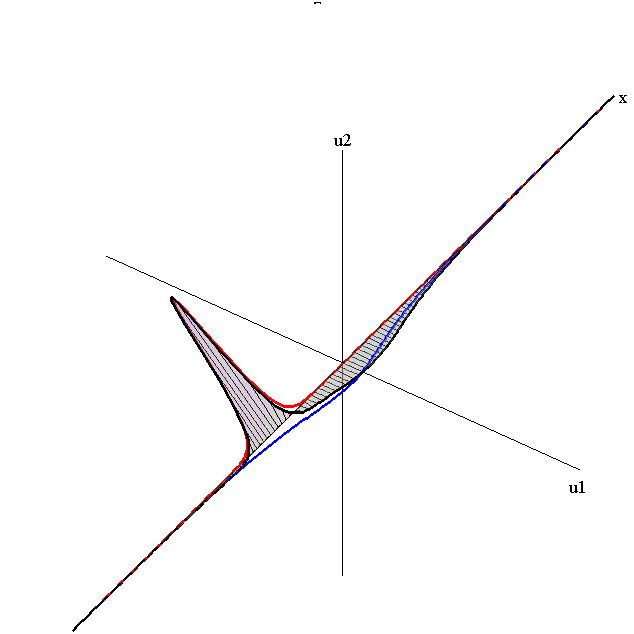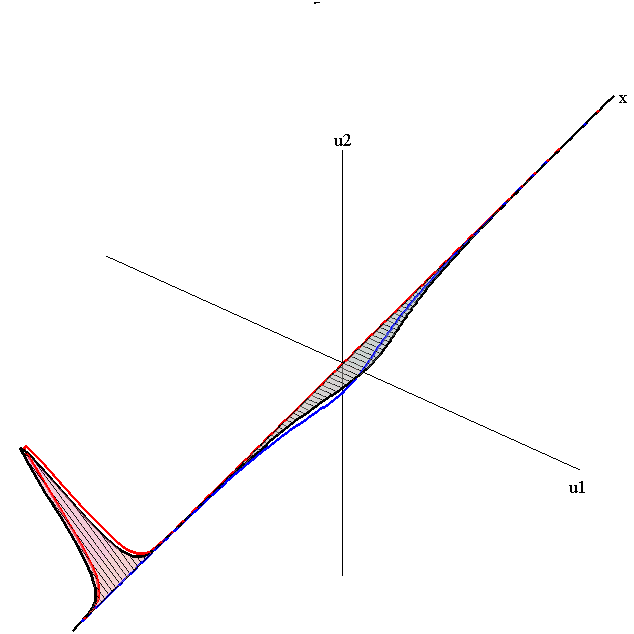
speed ratio: c1/c2 = 50
relative orientation angle: Δφ = 0.75 π
speed ratio: c1/c2 = 9
relative orientation angle: Δφ = π