Hirota Solitons

Hirota-mKdV Equation u_t + 24|u|²u_x + u_xxx = 0

There are two equivalent forms for the Hirota-mKdV equation:
(1) In complex-variable notation, u = u₁ + i u₂ satisfies

u_t + 24 uuu_x + u_xxx =0
(2) In vector notation, u = (u₁, u₂) satisfies

u_t + 24 u⋅u u_x + u_xxx =0

Travelling Wave Solution

Travelling waves are given by the special soliton solution

u(t,x)= (√c /2) exp(iφ)/cosh(√c ξ)
where c > 0 is the speed, −π ≤ φ ≤ π is the phase, and ξ = x−ct is a moving coordinate.

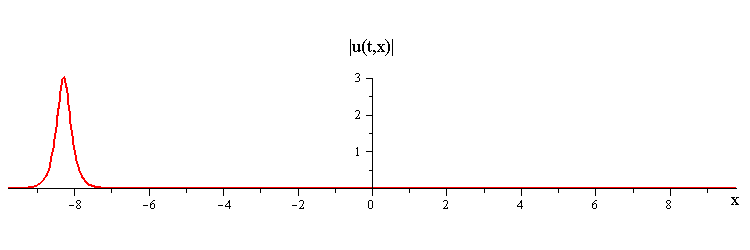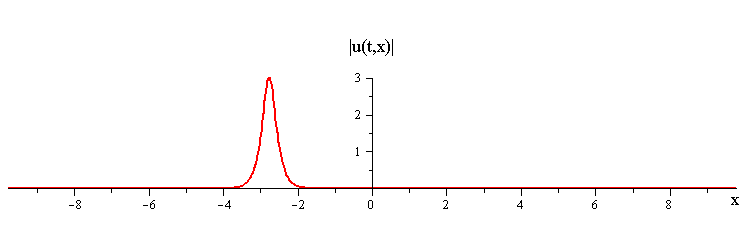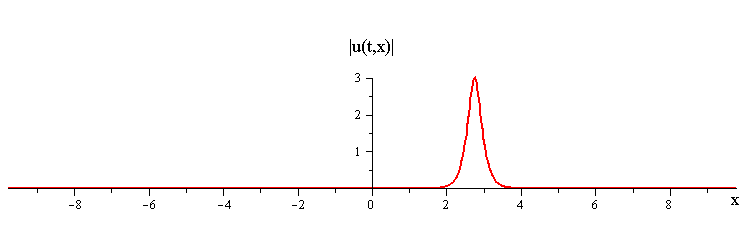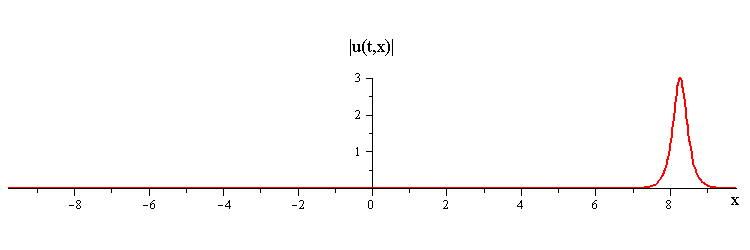
Colliding Travelling-Waves Solution

Collisions where a fast travelling wave with speed c₁ and phase φ₁ overtakes a slow travelling wave with speed c₂ and phase φ₂ are given by the special 2-soliton solution

u(t,x)= (c₁ − c₂)( √c₁ exp(iφ₁) cosh(√c₂ ξ₂) + √c₂ exp(iφ₂) cosh(√c₁ ξ₁) )/( 4 √c₁√c₂ cos(φ₁ − φ₂) + (√c₁ − √c₂)² cosh(√c₁ ξ₁ + √c₂ ξ₂) + (√c₁ + √c₂)² cosh(√c₁ ξ₁ − √c₂ ξ₂) )
where ξ₁ = x−c₁t, ξ₂ = x−c₂t are moving coordinates.

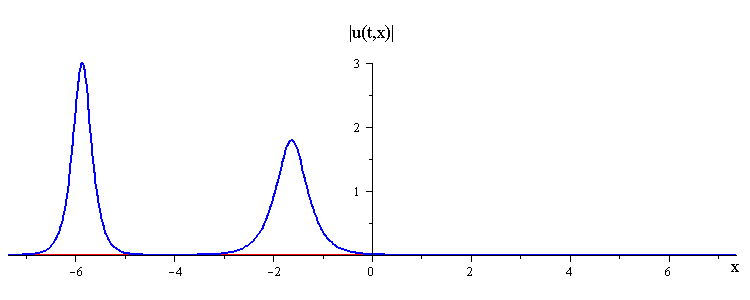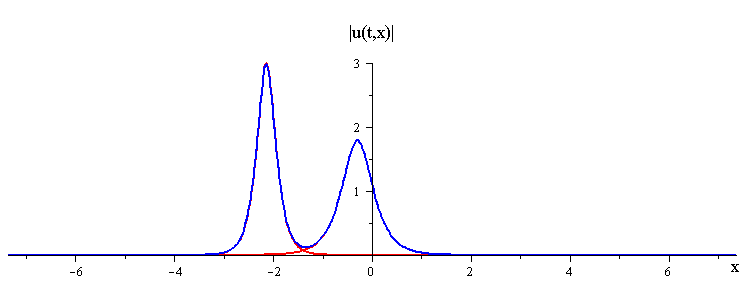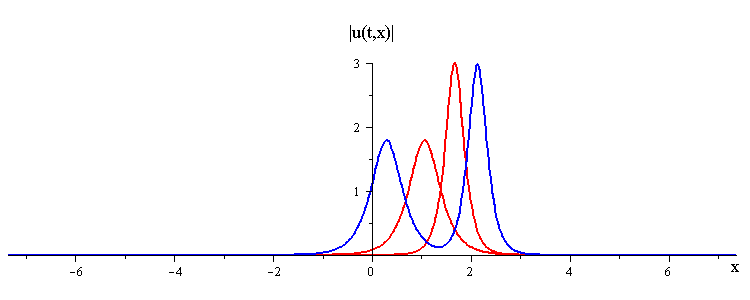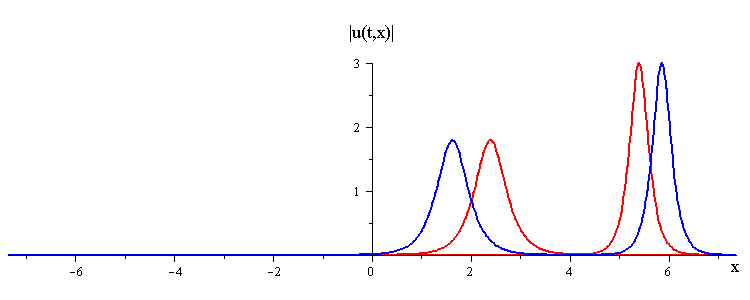
Overlay of Travelling-Wave Solutions and Corresponding Collision Solution

Hirota merge-split interaction
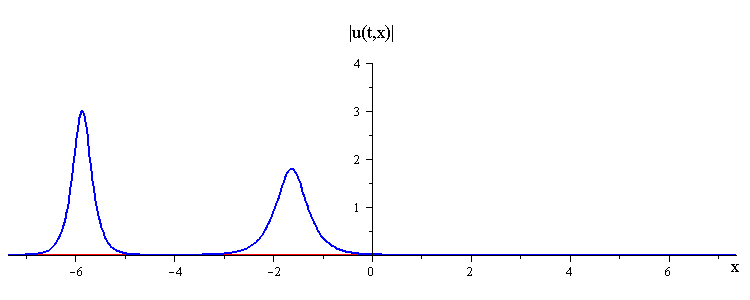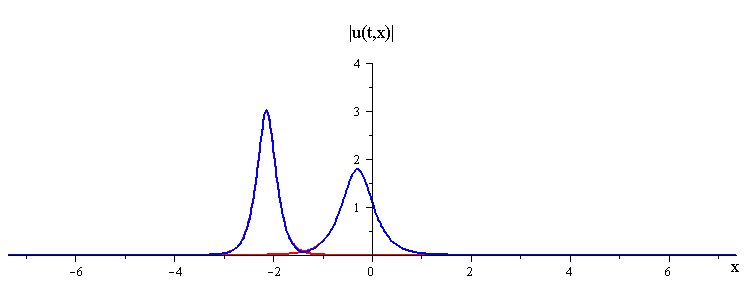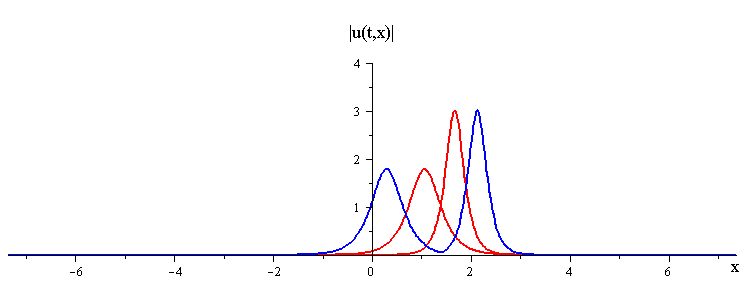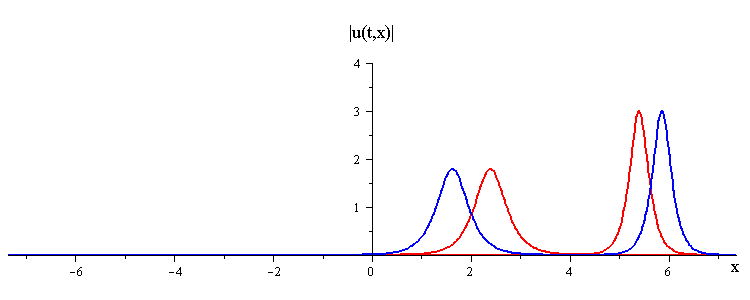
ratio of fast to slow wave speeds is c₁/c₂ = 2.8
difference in phases is |φ₁ − φ₂| = 0.75 π
(Click here to see the space time portrait)

Hirota bounce-exchange interaction ratio of fast to slow wave speeds is c₁/c₂ = 2.8
difference in phases is |φ₁ − φ₂| = 0.3 π
(Click here to see the space time portrait)


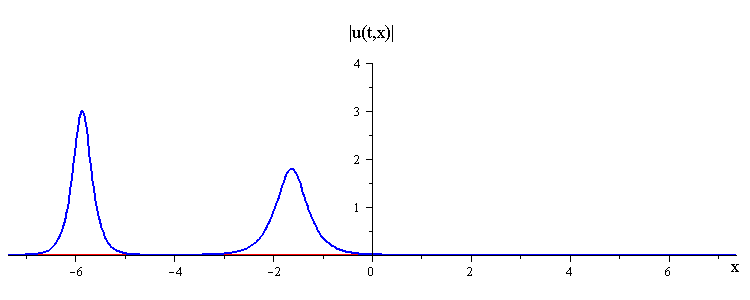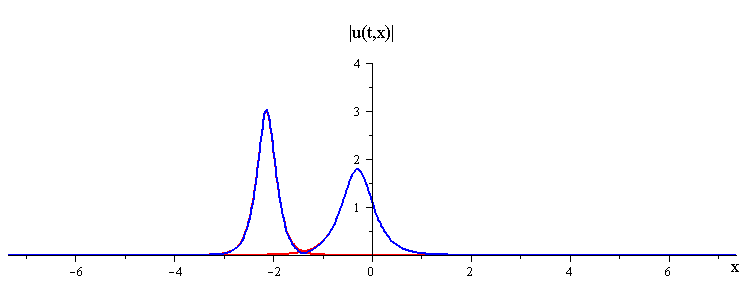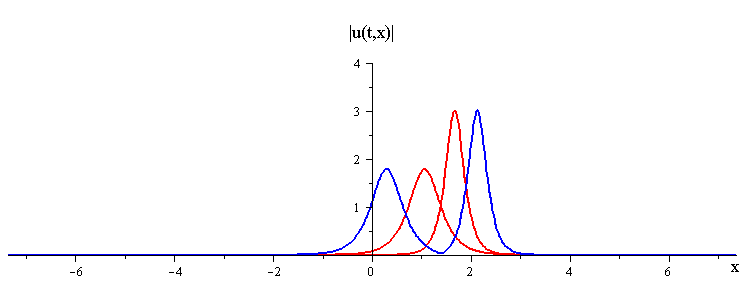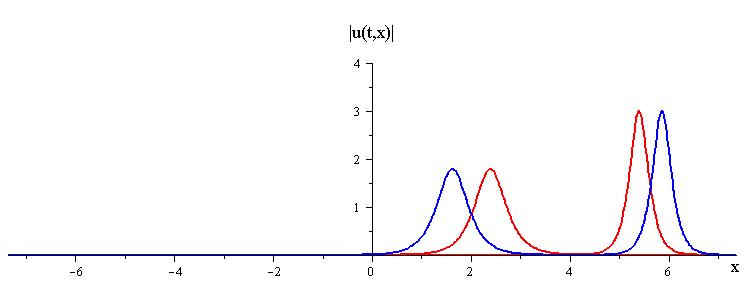Hirota critical-phase interaction ratio of fast to slow wave speeds is c₁/c₂ = 2.8
difference in phases is |φ₁ − φ₂| = 0.8689 π
(Click here to see the space time portrait)

Hirota absorb-emit interaction
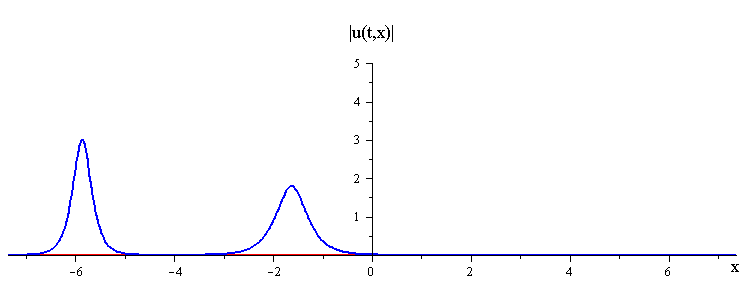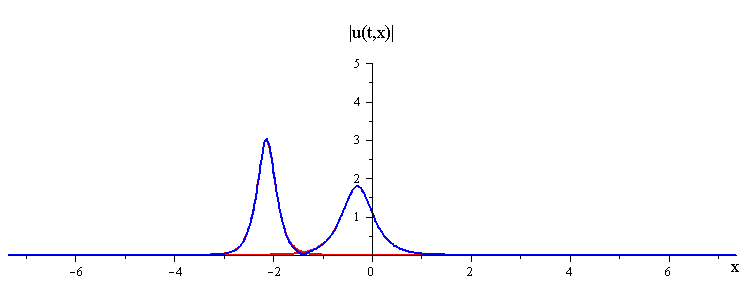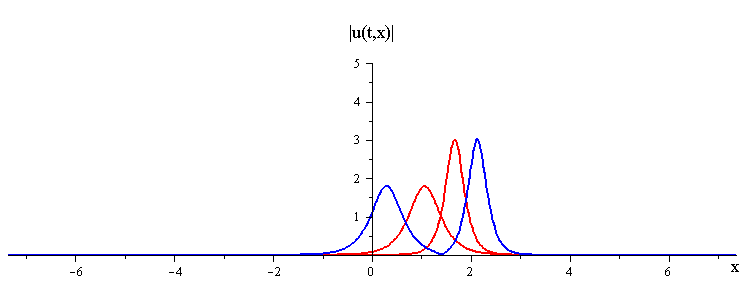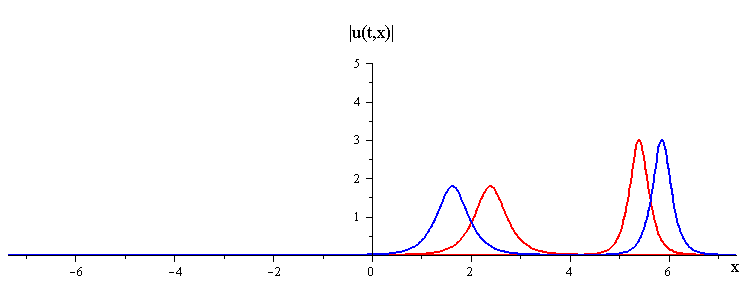
ratio of fast to slow wave speeds is c₁/c₂ = 2.8
difference in phases is |φ₁ − φ₂| = 0.95 π
(Click here to see the space time portrait)

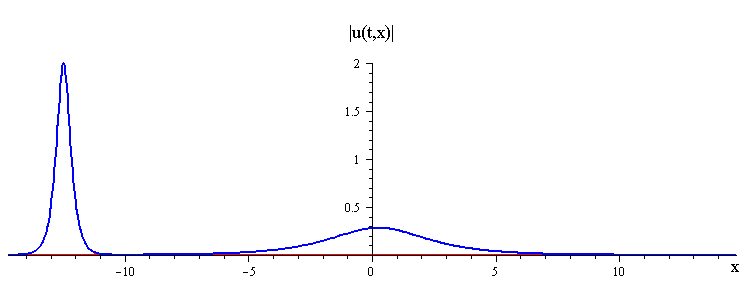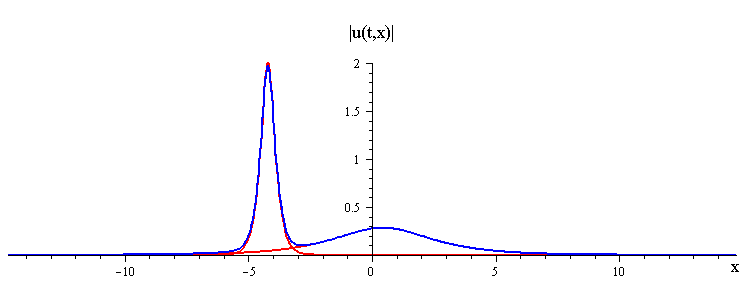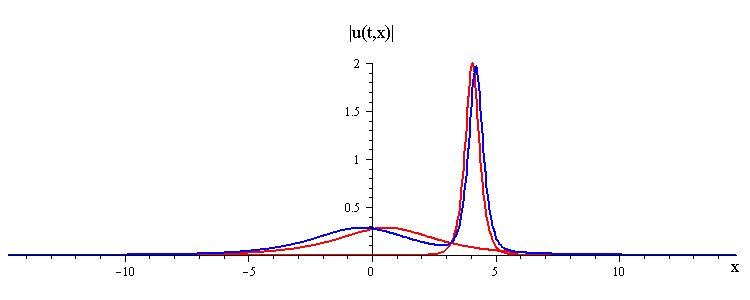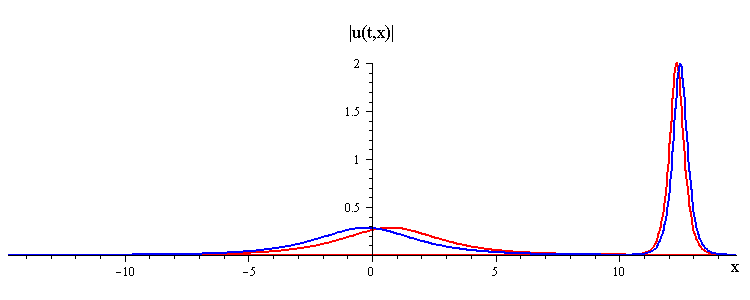Hirota merge-split interaction ratio of fast to slow wave speeds is c₁/c₂ = 50
difference in phases is |φ₁ − φ₂| = 0.3 π
(Click here to see the space time portrait)

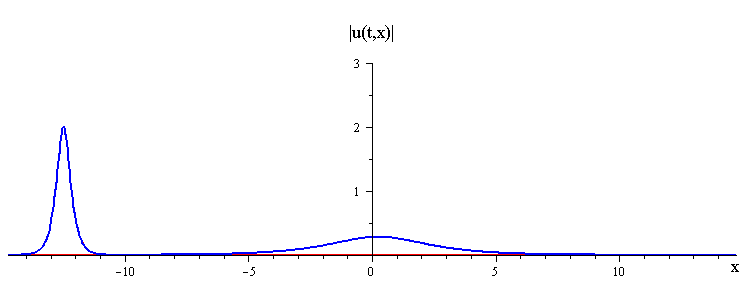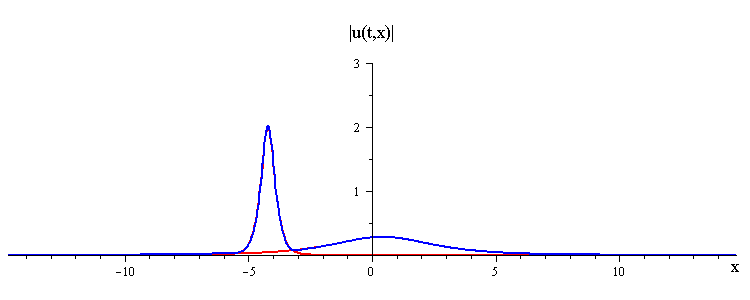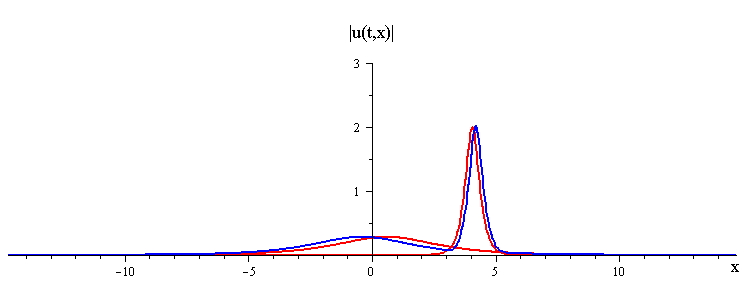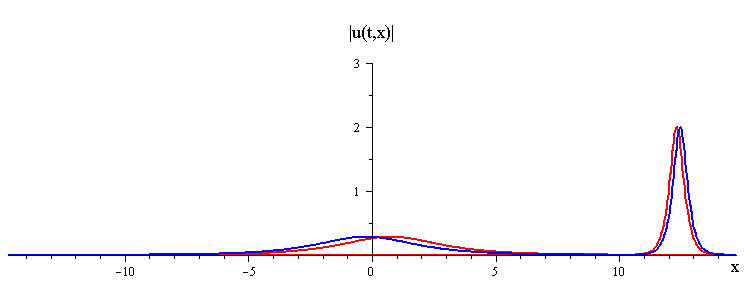Hirota critical-phase interaction ratio of fast to slow wave speeds is c₁/c₂ = 50
difference in phases is |φ₁ − φ₂| = 0.637 π
(Click here to see the space time portrait)

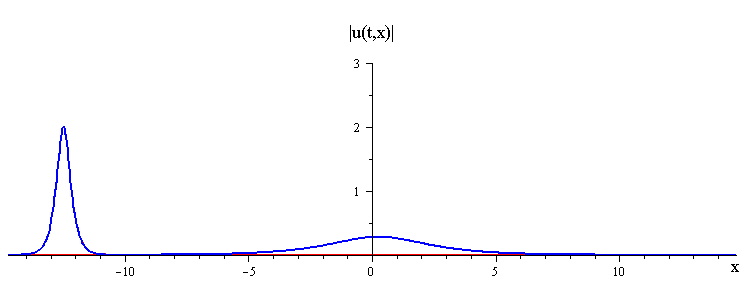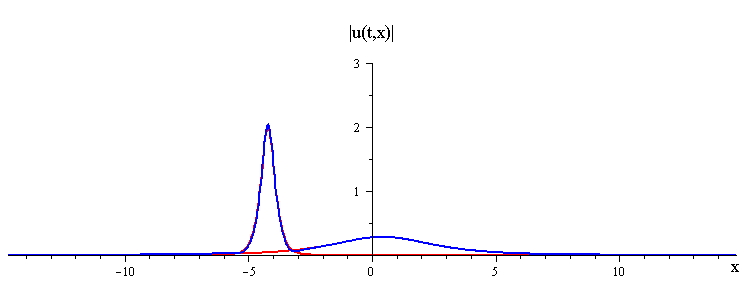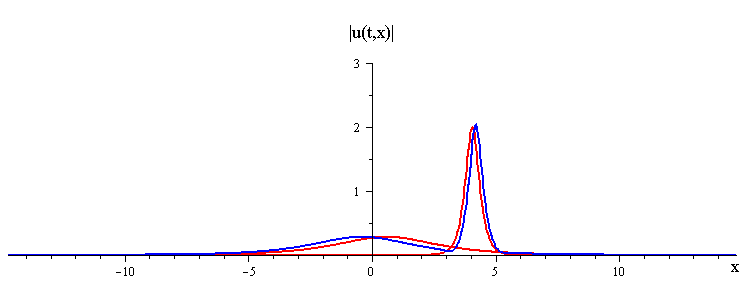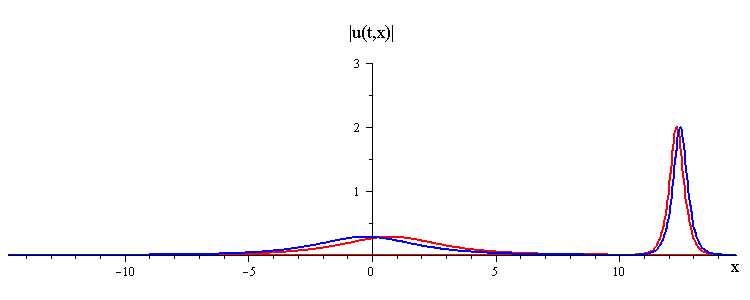Hirota absorb-emit interaction ratio of fast to slow wave speeds is c₁/c₂ = 50
difference in phases is |φ₁ − φ₂| = 0.75 π
(Click here to see the space time portrait)