mKdV Solitons
Modified KdV Equation ut + 24 u2ux + uxxx = 0
Travelling wave solutions of the general mKdV equation ut + αu2ux +βuxxx = 0 are non-singular only when the coefficients of the nonlinear convective term u2ux and the linear dispersive term uxxx have a relative positive sign, α/β > 0 (called the defocusing case). Up their relative sign, these coefficients α, β can be freely changed by a scaling transformation on the variables u, x, t. The conventional choice α = 24, β=1 eliminates awkward numerical factors in the expressions for single and multi soliton solutions.In contrast to the KdV equation, a reflection transformation u → −u is a symmetry for the mKdV equation. Every mKdV solution thereby has a mirror solution that differs only by a reflection (i.e. an overall ± sign).
1-Soliton Solution
The mKdV 1-soliton solution iswhere c > 0 is the wave speed, s = ±1 is an up/down orientation of the wave profile, and ξ = x−ct is a moving coordinate.
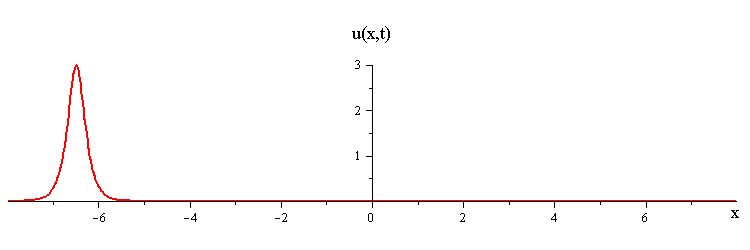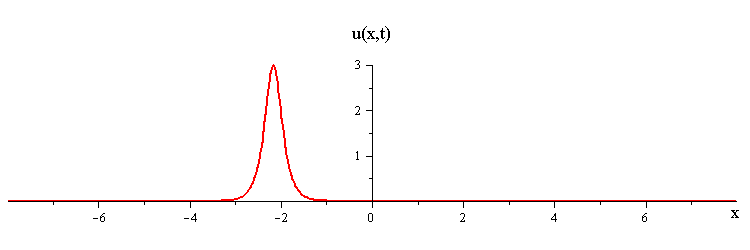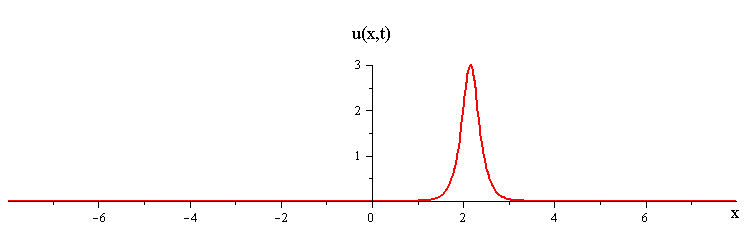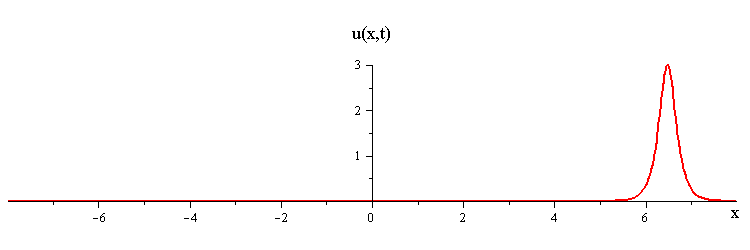
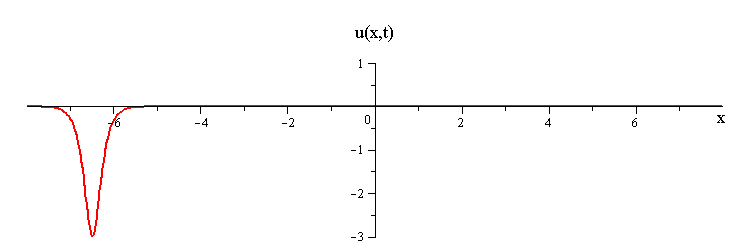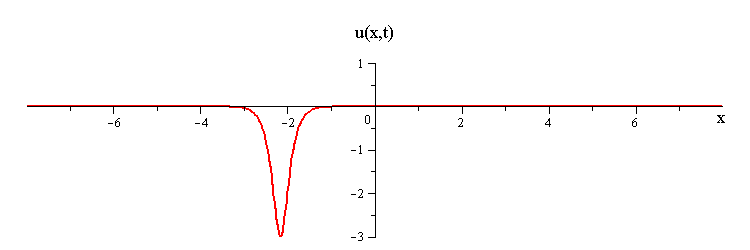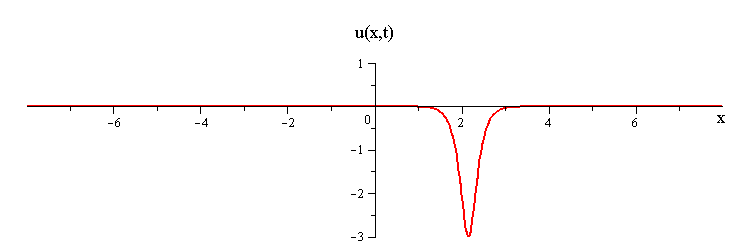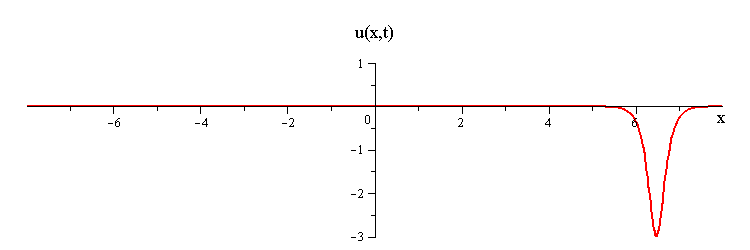
2-Soliton Solution
The mKdV 2-soliton solution is+ (√c1 − √c2)2 cosh(√c1 ξ1 + √c2 ξ2) + (√c1 + √c2)2 cosh(√c1 ξ1 − √c2 ξ2) )
where c1 > c2 > 0 are the wave speeds, s1 = ±1 and s2 = ±1 are the wave orientations, and ξ1 = x−c1t, ξ2 = x−c2t are moving coordinates.
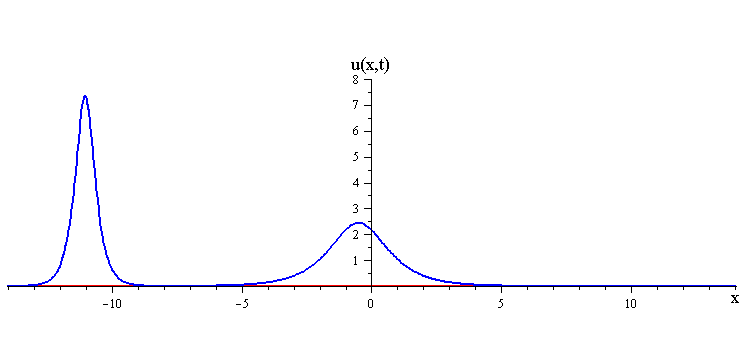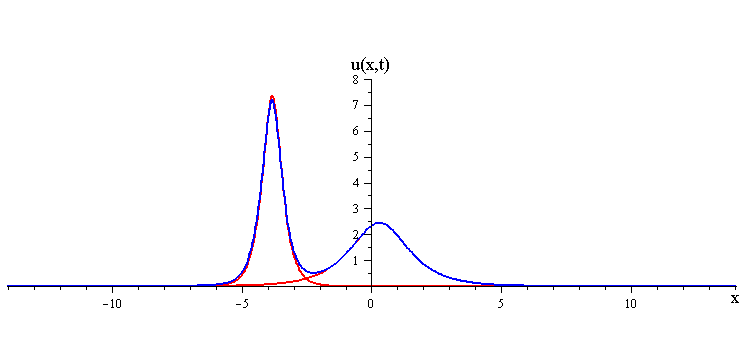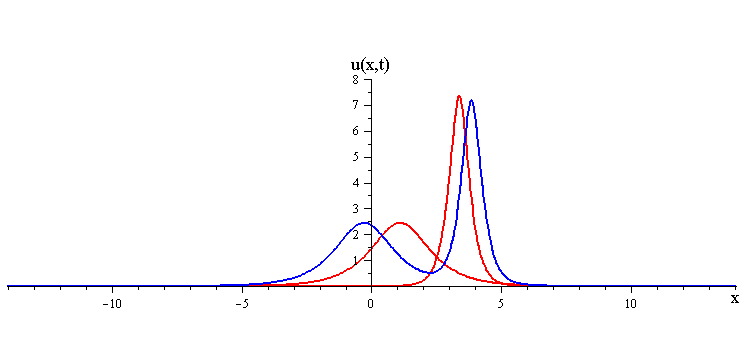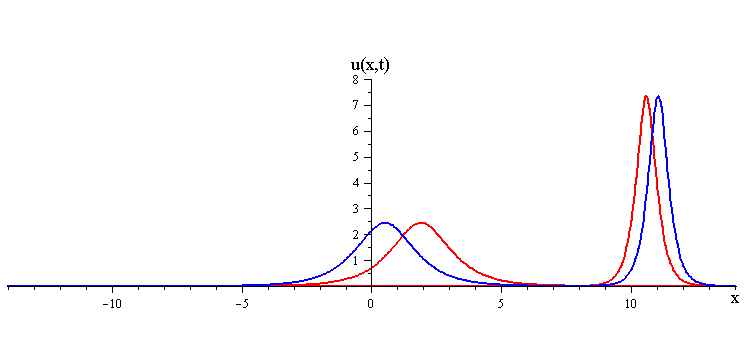
As t → ±∞, the 2-soliton solution has the asymptotic form of a linear superposition of travelling waves (i.e. single solitons) with speeds c1 and c2 and up/down orientations s1 = ±1 and s2 = ±1. The two waves wave collide such that the moment of greatest nonlinear interaction occurs at t = 0 when the profile is symmetric is symmetric around x = 0. The shape of this profile u(x,0)= u(−x,0) characterizes the nonlinear interaction of the waves in the collision.
When the two waves have the same orientation s1 = s2 = ±1, their nonlinear interaction depends on whether their speed ratio is greater or less than a critical value c1 / c2 = (7 + 3√5)/2 (as determined from the condition that the convexity of u(x,0) vanishes). If the speed ratio is c1 / c2 > (7 + 3√5)/2, the waves interact nonlinearly by first merging at x = t = 0 and then splitting apart. In this case the profile u(x,0) has a single peak at x = 0 and an exponentially diminishing tail as x → ±∞.
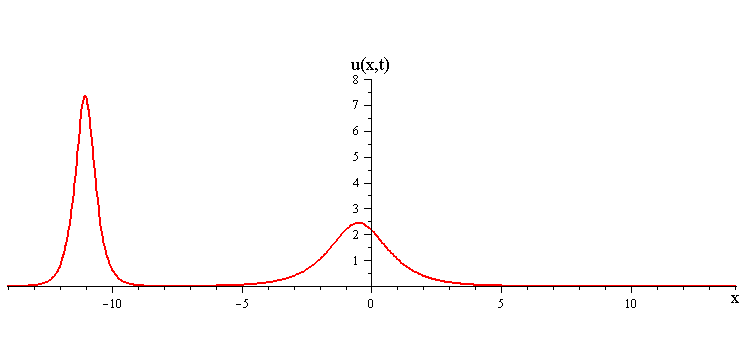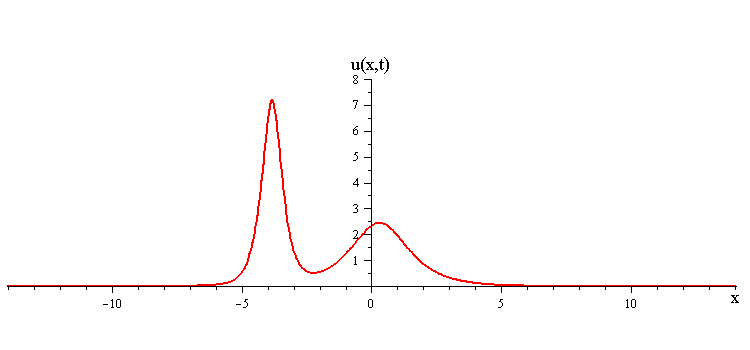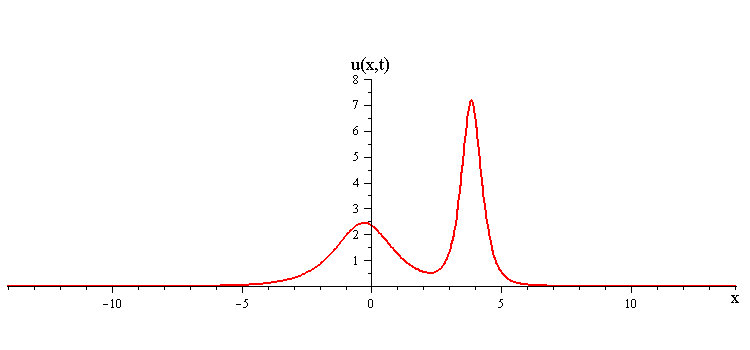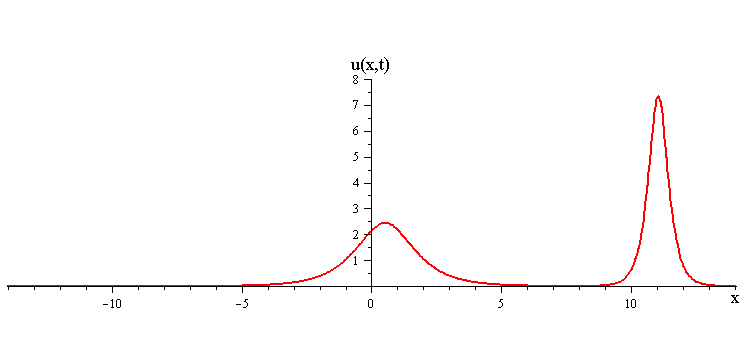
ratio of fast to slow wave speeds is > (7 + 3√5)/2 ≅ 6.85
(Click here to see the space time portrait)
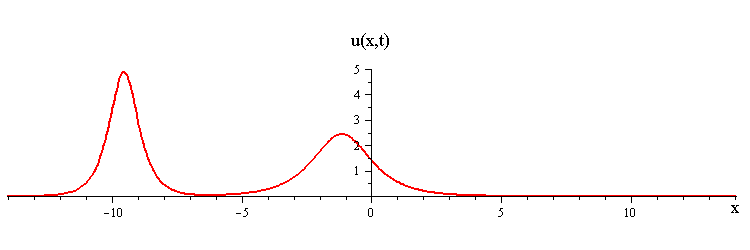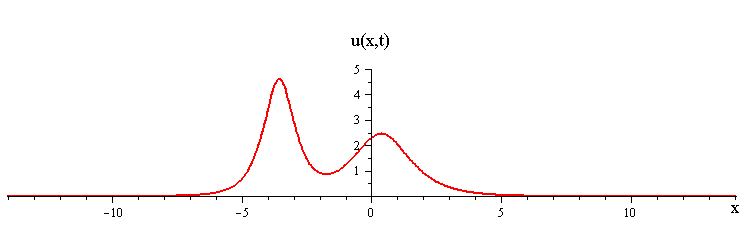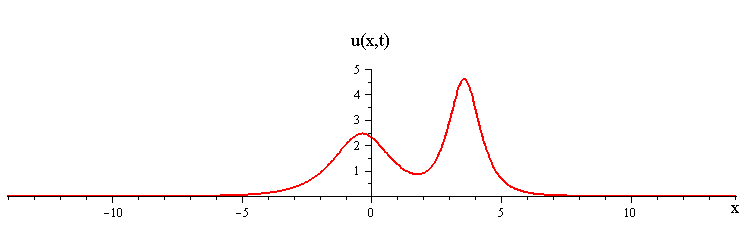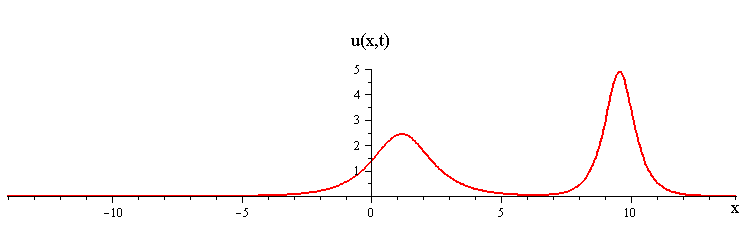 ratio of fast to slow wave speeds is < (7 + 3√5)/2 ≅ 6.85
ratio of fast to slow wave speeds is < (7 + 3√5)/2 ≅ 6.85
(Click here to see the space time portrait)
In contrast when the two waves have opposite orientations s1 = −s2 = ±1, they have a completely different nonlinear interaction where the slow wave gradually is first absorbed and then emitted by the fast wave. Their profile u(x,0) in this case has a central peak at x = 0 plus a pair of side peaks around x ≠ 0 with an exponentially diminishing tail as x → ±∞.
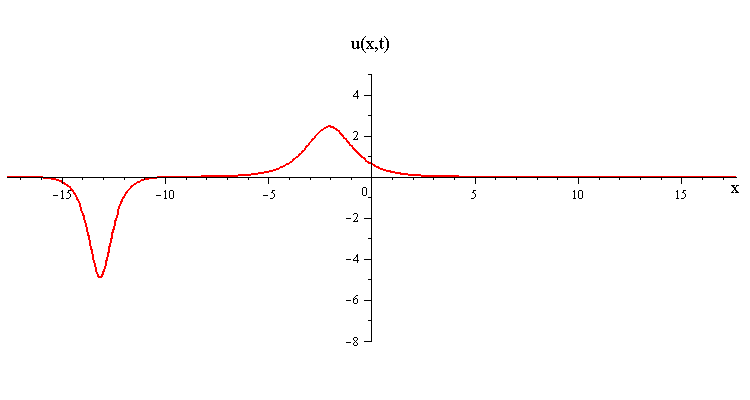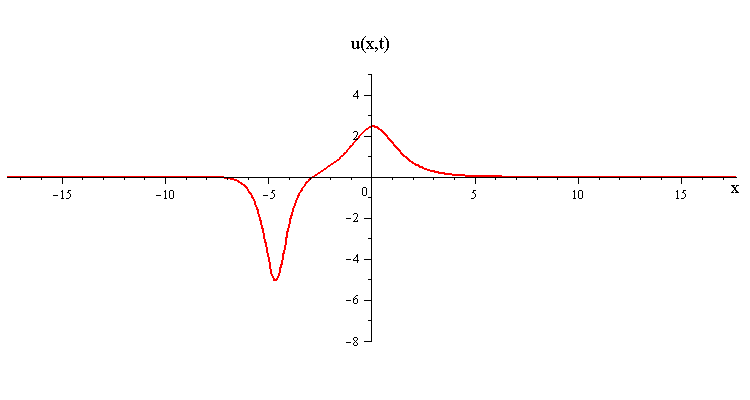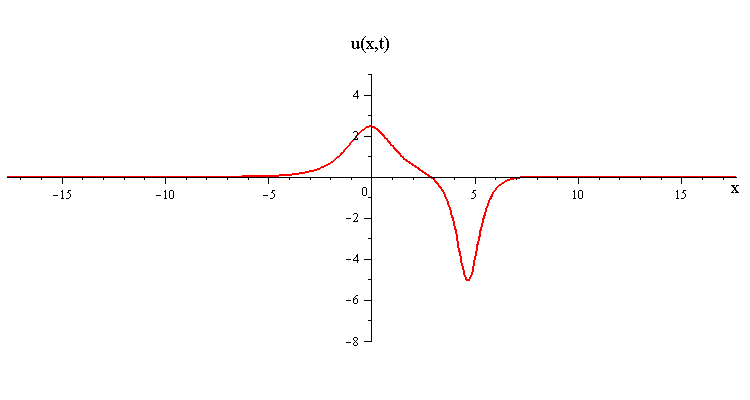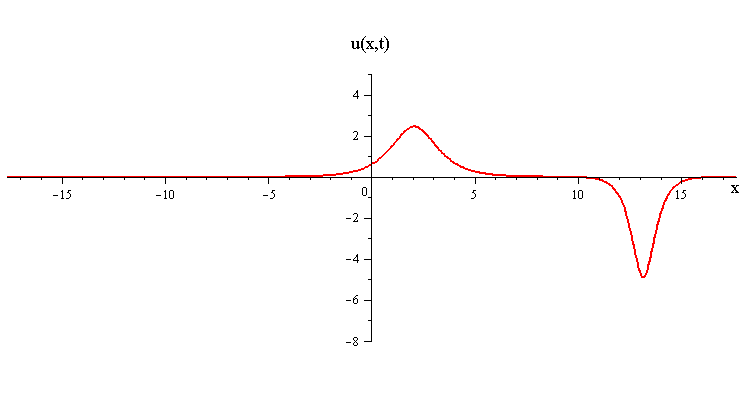
(Click here to see the space time portrait)
Overlay of 1-soliton solutions and corresponding 2-soliton solution
 ratio of fast to slow wave speeds is > (7 + 3√5) / 2 ≅ 6.85
ratio of fast to slow wave speeds is > (7 + 3√5) / 2 ≅ 6.85
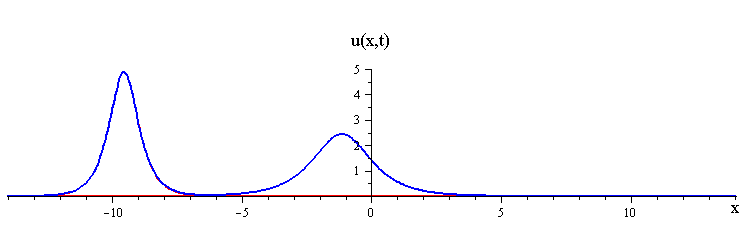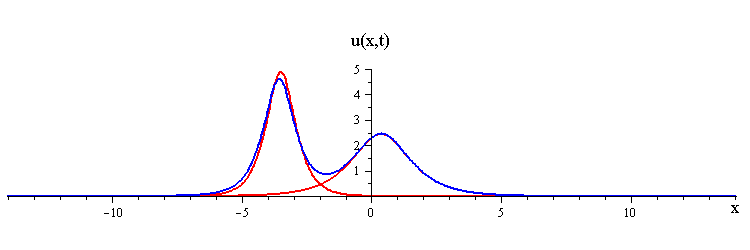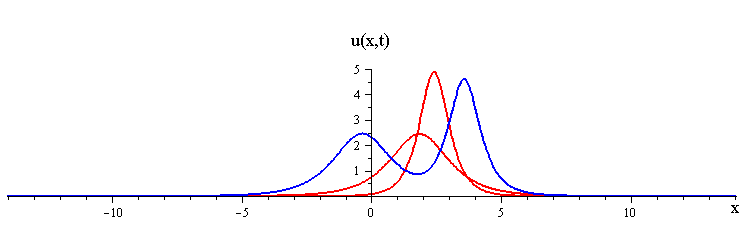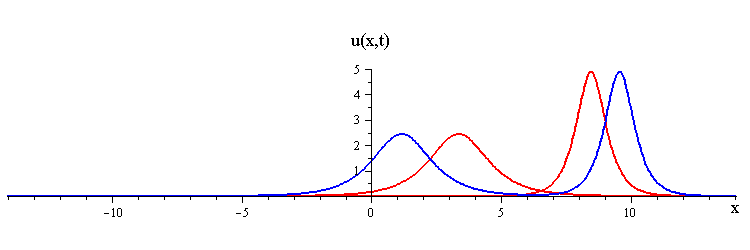
ratio of fast to slow wave speeds is < (7 + 3√5) / 2 ≅ 6.85
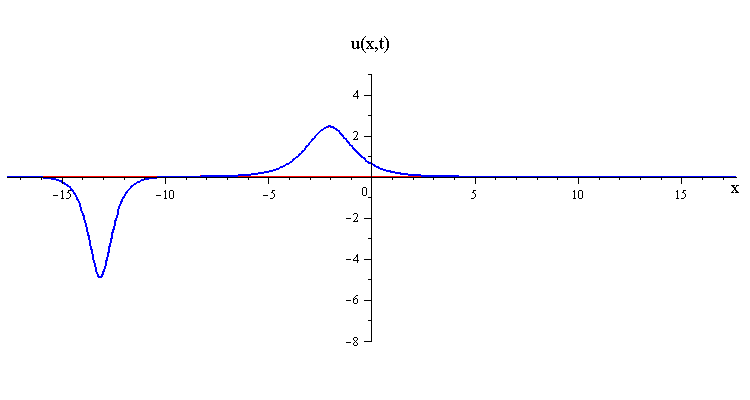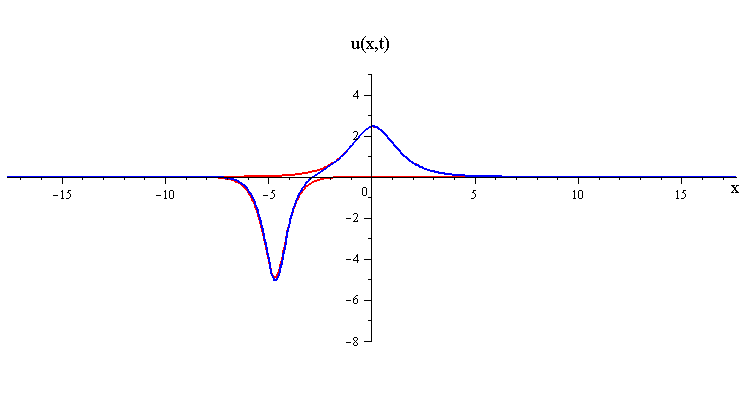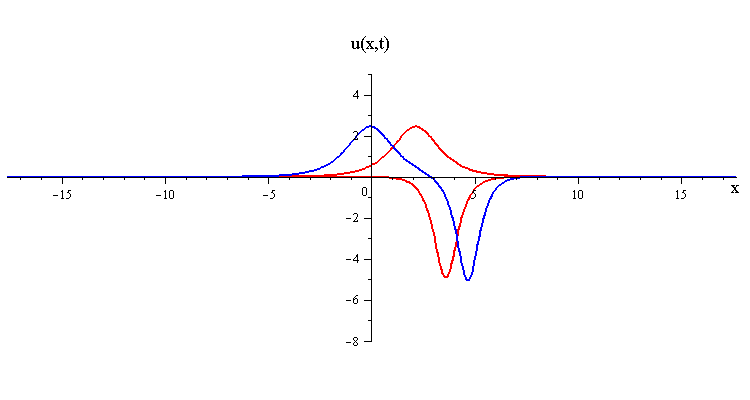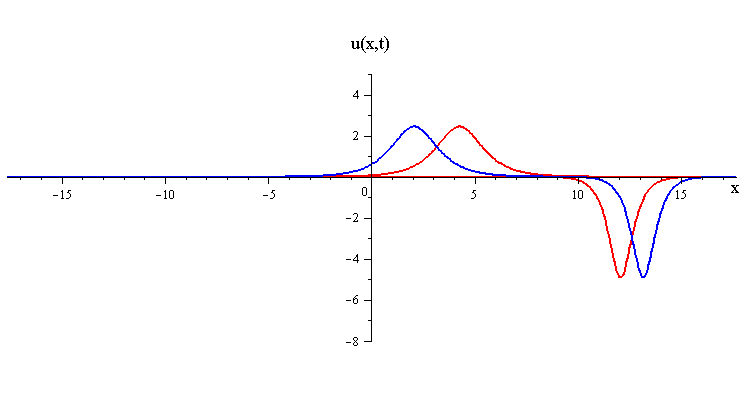
and the slower wave gets shifted backward by
where √c1 > √c2 > 0. These position shifts are the same as those for the KdV 2-soliton solution.