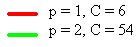Nonlinear Wave Equations

There are many different nonlinear wave equations. Some types of equations have solutions that display singularities or gradient blow-ups, while other types of equations have smooth dispersive solutions (decaying in time and space) or, in some cases, stable traveling wave solutions.

The Convective Wave Equation

The general form of the convective wave equation is u_t + c(u)u_x = 0 where c(u) is the wave speed given by a function of the wave amplitude u. If the wave speed is a constant (i.e. c′(u) = 0), this equation has traveling wave solutions. For non-constant wave speeds c(u) there are no traveling wave solutions, instead gradient blow-ups occur.

The simplest example is c(u) = u^p which depends on a positive integer p, giving a nonlinear convective equation

u_t + u^pu_x = 0
Solutions u(x, t) describe nonlinear waves whose profile eventually becomes multi-valued (i.e. there is a gradient blow-up).

u(x, 0) = sech²(x)

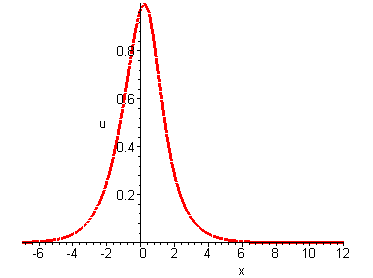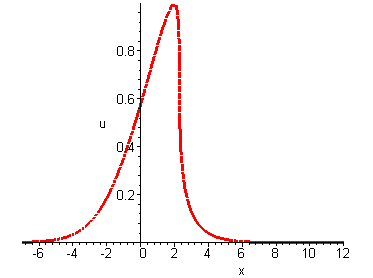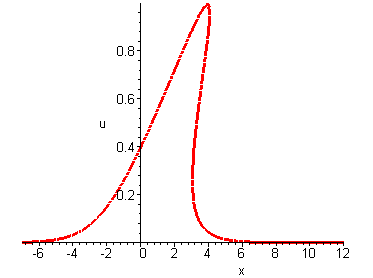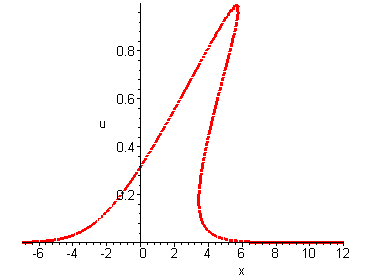
p = 1
Naturally the question arises, how can this wave equation be modified to possess stable traveling wave solutions? Stable traveling waves with localized profiles (having rapid spatial decay) are called solitary waves.

The Dispersive Wave Equation

Can dispersion balance nonlinearity? The simplest dispersive wave equation is

u_t + u_xxx = 0
Its solutions u(x, t) have the general form of an integral superposition of oscillatory waves exp(ik³t + ikx) with frequency ω = k³ / 2π and wavelength λ = 2π / k for arbitrary k. The amplitude of these oscillatory waves is the Fourier transform of the initial profile u(x, 0). Because oscillatory waves of different frequency propagate at different speeds, there are no localized travelling wave solutions. Instead solutions u(x, t) describe dispersive waves whose profile develops an oscillatory decaying tail.

u(x, 0) = sech²(x)

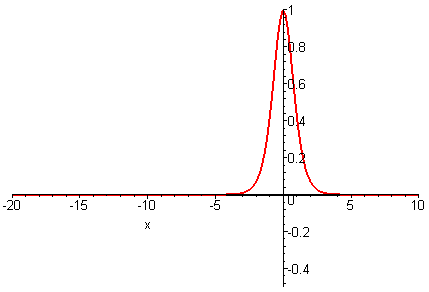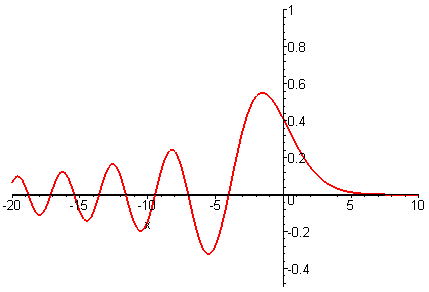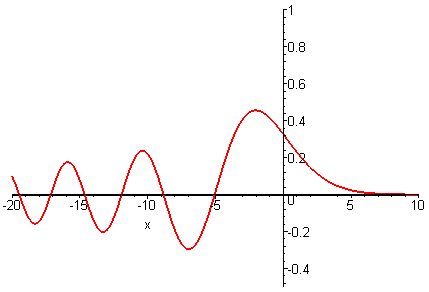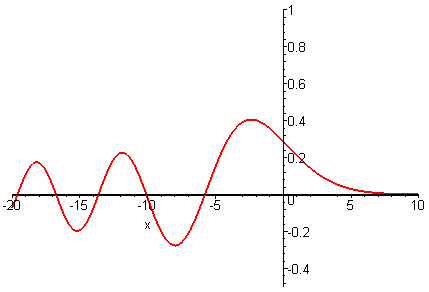
Nonlinearity and Dispersion

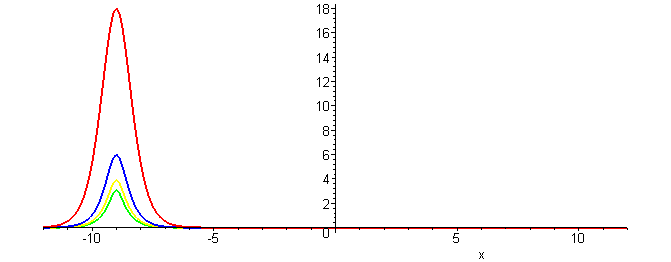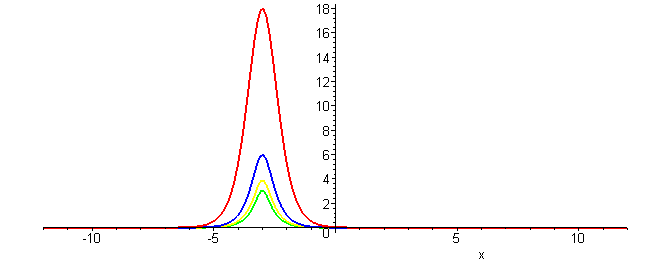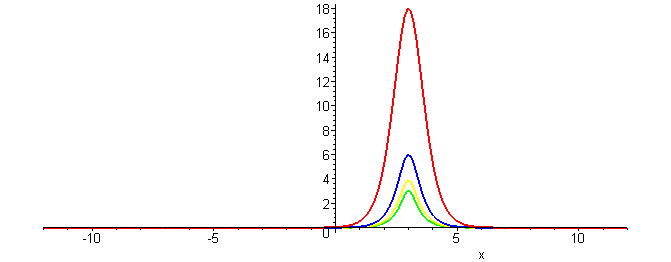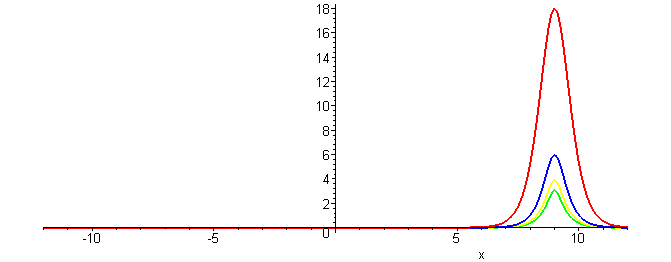
The physical feature of balancing dispersion against nonlinearity leads to solitary wave solutions. Adding the dispersive term to term u_xxx to the nonlinear convective equation gives the Generalized KdV equation

u_t + u^pu_x + u_xxx = 0

where p is a positive integer.

Localized traveling wave solutions (solitary waves) of the GKdV equation have the form
u(x,t)= ( (p+1)(p+2)c/2 )^1/p sech^2/p( p√c (x−ct)/2) )

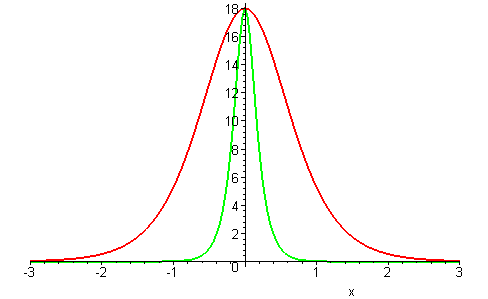
with a constant wave speed c > 0. The following plots depict how changing the degree of nonlinearity (p) affects the wave profile.

Waves having the same wave speed have a decrease in wave height as the nonlinearity increases.
Waves of the same height (but different speeds) have a steeper and narrower profile.