Generalized KdV Interactions
What happens when nonlinear waves interact?
In linear interactions of localized travelling waves, the initial wave profiles get superimposed as the waves collide and reappear as the waves move apart. Does the GKdV equation exhibit similar behavior for colliding waves?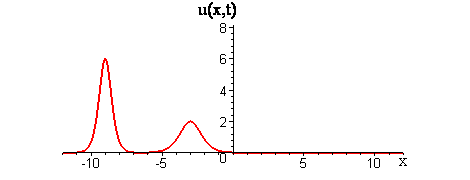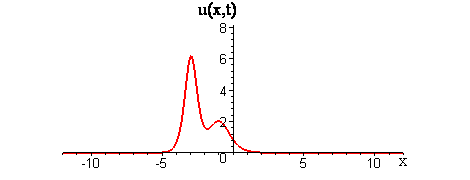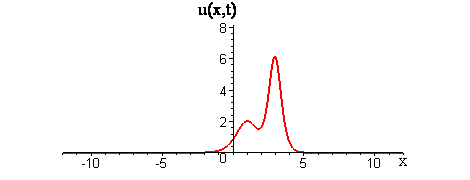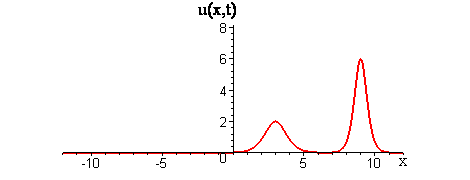
The KdV Equation ut + uux + uxxx = 0
Among all of the GKdV-p equations ut + upux + uxxx = 0, the weakest nonlinearity occurs for the case p = 1, which is the KdV equation.KdV travelling waves have the feature that their shape depends on their speed. Faster waves are taller and narrower, while shorter waves are shorter and broader. The ratio of height to width for a KdV travelling wave with speed c > 0 is approximately 3c : 2 / √c.
Travelling wave solutions of the KdV equation (p = 1)
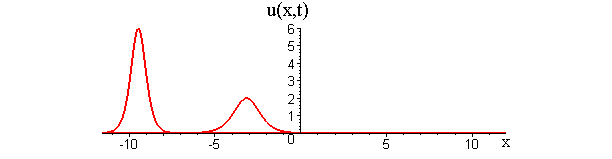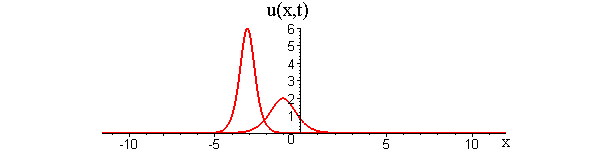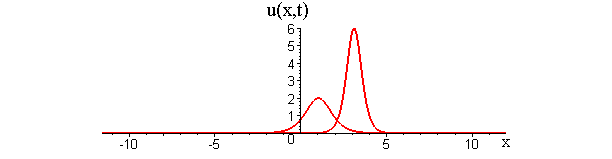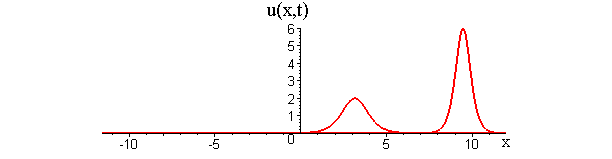
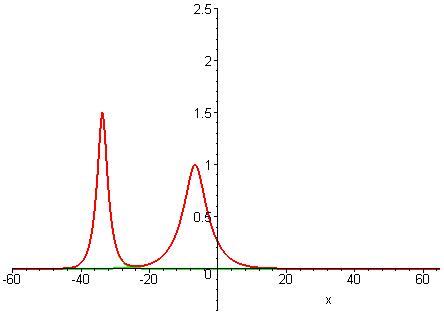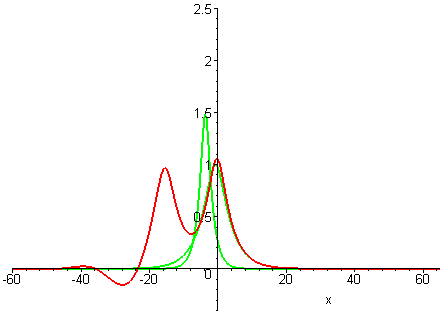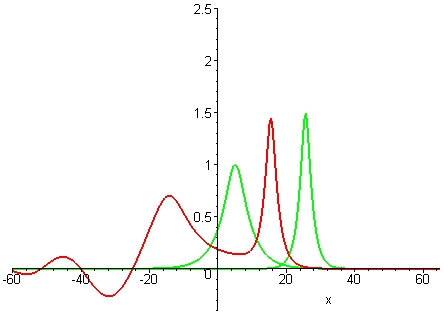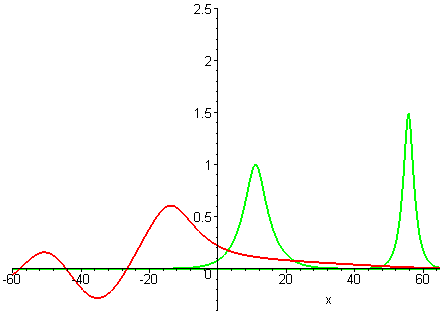
Collisions of KdV travelling waves are described by solutions whose initial profiles are superpositions of two (or more) individually travelling waves with different speeds. In these solutions, the waves undergo a nonlinear interaction that differs significantly compared to a linear superposition.
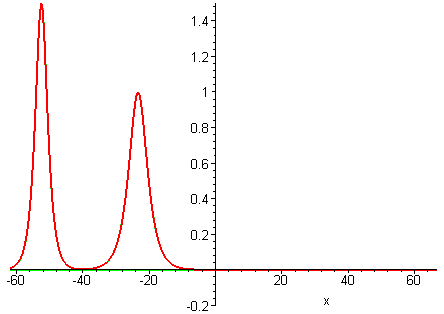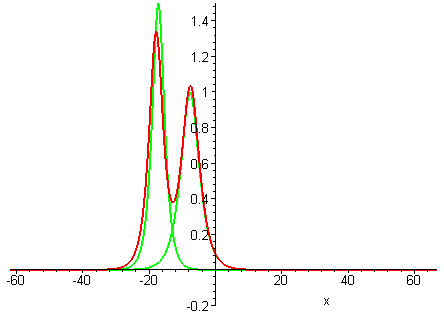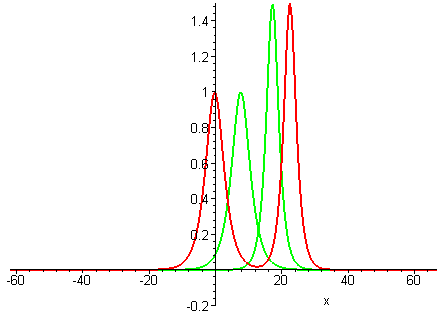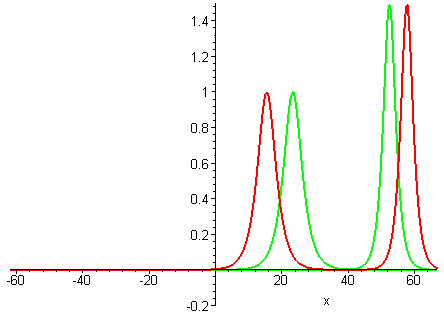
There are two kinds of collision behaviour, depending on the ratio of the initial wave speeds where c1 and c2 are the respective speeds of the faster and slower waves. When the speed ratio is c1 / c2 > 3, the waves first merge and then split apart into their previous shape and speed. In contrast, when the speed ratio is c1 / c2 < 3, the waves bounce and exchange both their shape and speed.
KdV (p = 1) colliding wave solution with speed ratio c1 / c2 > 3
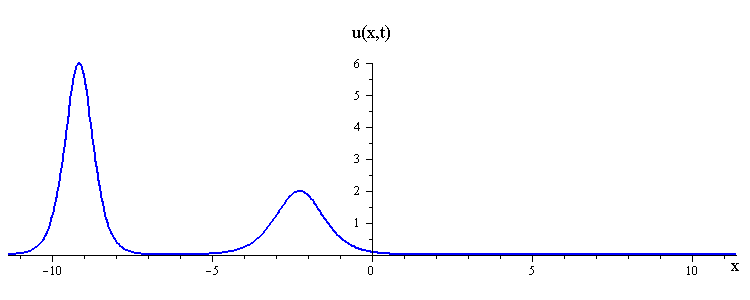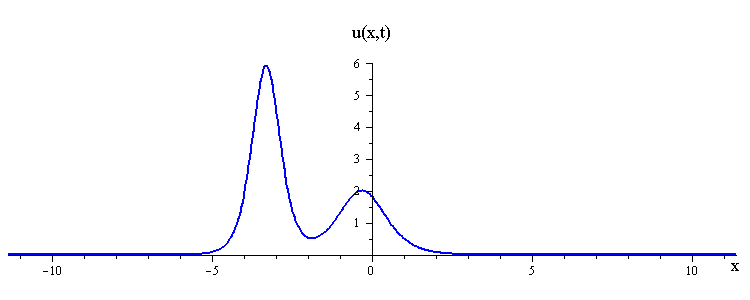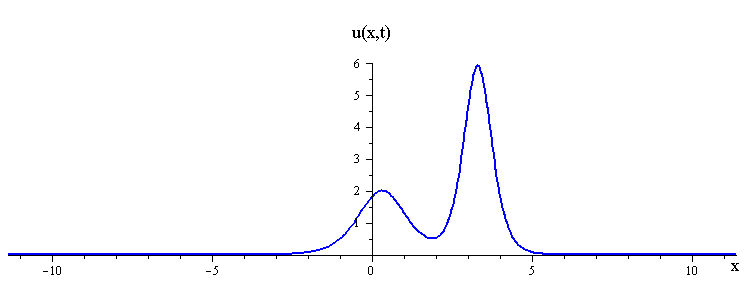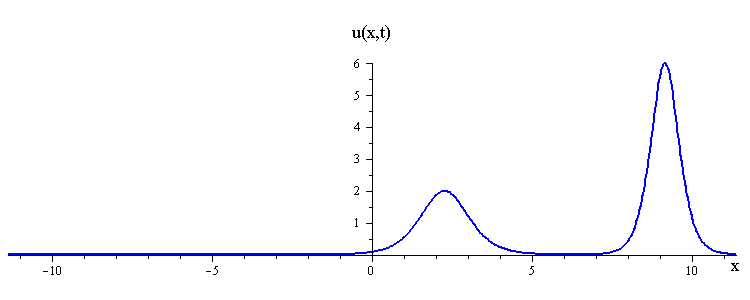
KdV (p = 1) colliding wave solution with speed ratio c1 / c2 < 3
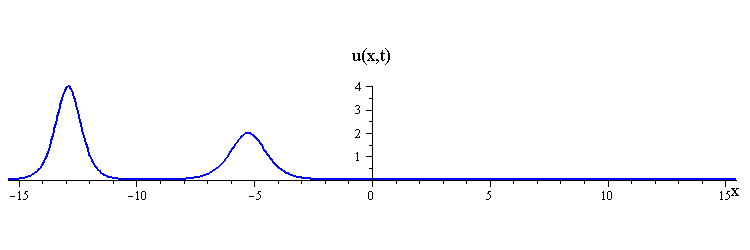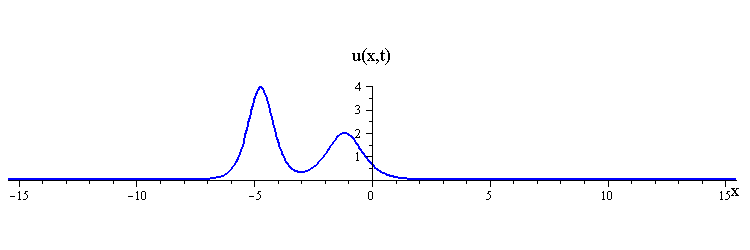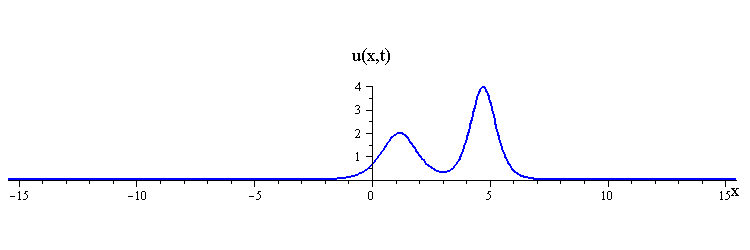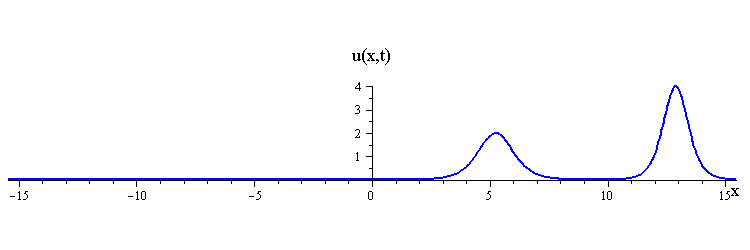
Remarkably, in all collisions, the only remnant of the nonlinear interaction is a shift in the positions of the two waves.
Colliding wave solutions of the GKdV-p equation for p = 2, 3, 4
A natural question is whether colliding wave solutions of all GKdV-p equations exhibit the same interaction properties as KdV travelling waves.Collisions of travelling waves with the next weakest nonlinearities p = 2, 3, 4 are depicted in the following plots. The GKdV-2 case is known as the modified KdV (MKdV) equation.
GKdV-3
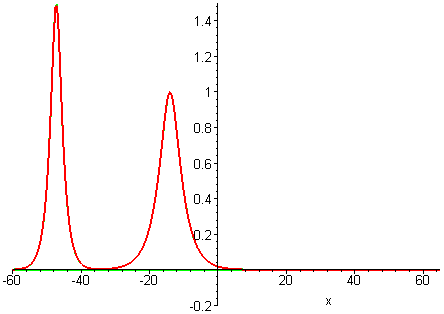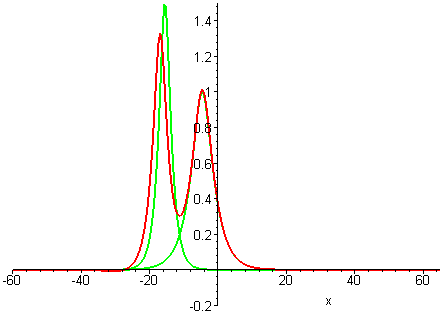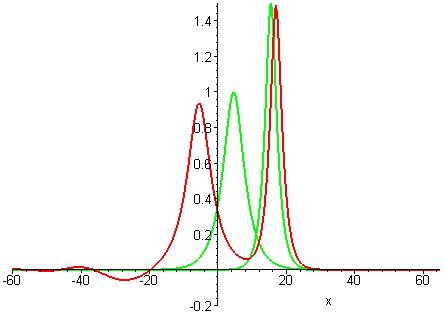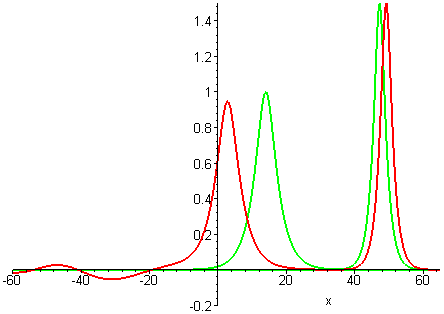
GKdV-4